
I en fersk KOFA-sak antyder KOFA at en oppdragsgiver har gitt skjønnsmessig poeng på pris. Men må det være det som har skjedd, egentlig?
Hold deg fast, for nå skal vi litt inn i matematikkens verden. Vi skal forsøke å gjøre det så smertefritt som mulig, men nå er du forberedt!
Tenk deg at du har fått inn to tilbud med to like priser, for eksempel 500.000 og 500.000. Hvordan skal du gi poeng til disse to prisene?
Det er vel ganske greit. Begge prisene er jo faktisk den laveste prisen du er tilbudt, så dermed får begge prisene maksimal poengsum. For eksempel 10 poeng til hver. Hvilken pris liker du best? Den på 500.000 eller den på 500.000?
Var et dumt eksempel, sier du? Nåja..
La oss nå tenke oss at en av prisene er høyere enn den andre. Da må vi inn med matematikk, og selv de klokeste hodene i landet vil nå krype ned i hver sin skyttergrav og hevde at de har rett.
Kjør debatt!
La oss si at prisene i stedet er 500.000 og 950.000.
I den ene skyttergraven vil noen rope «forholdsmessig metode gir oss en score på 10 mot 5,26 poeng!».
I den andre skyttergraven vil noen skrike «FEIL! Lineær metode gir oss en score på 10 mot 0,99 poeng!!»
Oppe på jordet, mellom skyttergravene rusler det en ku, som sier «Mø!».
Hvem har rett? De forholdsmessige? De lineære? Alle er vel ihvertfall skjønt enige om at kua tar feil. Svaret kan umulig være «Mø!».
Tilbake til virkeligheten, og til KOFA-sak 2024/1006. I denne saken kom det inn to priser, på henholdsvis 500.000 og 950.000. Den laveste prisen fikk 10 poeng, og den andre fikk… hold deg fast: «Mø!» poeng.
Hva behager?
Nei, den fikk ikke «Mø!» poeng, men i feltet for poengscore kunne det nok like gjerne stått «Mø!» for KOFA skjønte ingenting.
Det uforståelige tallet 7
I feltet sto det «7». Den laveste fikk 10 poeng, og den høyeste fikk 7 poeng.
Hvordan i all verdens dager kommer man fram til syv poeng? De to lagene klatrer ut av hver sin skyttergrav, og klør seg i hodet. Syv poeng? Hvilken formel er det?
KOFA mener det ikke er noen formel i det hele tatt. De skriver kort og godt at «ved bruk av en forholdsmessig metode hadde valgte leverandør fått 5,26 poeng, og ved en lineær metode 0,99 poeng. Etter nemndas syn kan det vanskelig forklares hvordan innklagede har regnet og kommet frem til tallet 7 for valgte leverandørs pris».
Så hva har skjedd?
Det er ihvertfall klart at en helt skjønnsmessig poengsetting av pris er problematisk. Hvor mye dyrere «synes du» at 950.000 er, sammenlignet med 500.000?
Men er det det som har skjedd i denne saken? Vel, det er ihvertfall ikke vanskelig å finne en formel som gir oss det svaret vi ønsker oss – på en matematisk måte.
Regresjon gir svaret på alt
Vi kan ta i bruk noe som kalles regresjon. Det vil si at man leter etter en formel som passer med datapunktene. I dette tilfellet er datapunktene 10 og 7. Hvilken formel kan man lage som gir deg disse svarene?
Vi kan ikke bruke formelen 10-10x(Pe-Pb)/Pb, som er formelen for lineær beregning av pris. Den vil altså gi deg tallet 0,99.
Vi kan heller ikke bruke formelen 10xPb/Pe, som er formelen for forholdsmessig beregning av pris. Den ville altså gitt deg tallet 5,26.
Begge disse formlene er hentet fra DFØs veileder for evaluering.
Men det finnes en formel, ja kanskje til og med flere. Du kan for eksempel bruke formelen (10xPb/Pe)^0,556. Denne formelen vil gi deg tallet 7 hvis laveste pris er 500.000 og den andre prisen er 950.000. La oss kalle det «Mø-metoden», etter kua som ingen skjønte noe av i eksemplet vårt.
Hvor raskt faller en sten?
I realiteten styrer vi rett og slett hvor raskt grafen faller når prisene blir høyere. Altså den grafen som faller som en stein ved lineær metode, og betydelig saktere ved forholdsmessig metode. Ved mø-metoden, faller kurven enda litt saktere, men bare litt. Her kan du se alle tre:
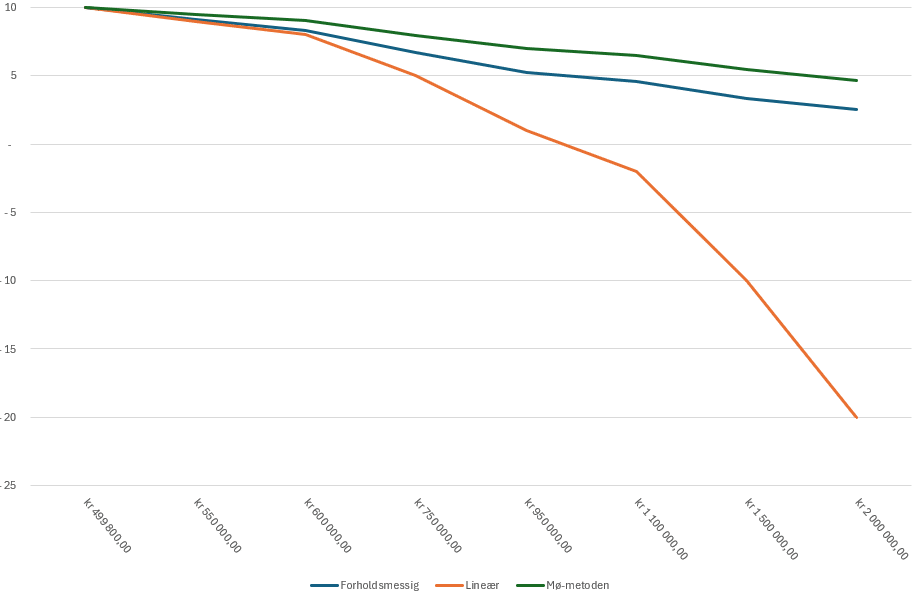
Så med litt matematikk, har kua fått sin egen skyttergrav.
Og hva hjelper dette oss? Ikke mye, men nå forstår du at det finnes en formel for alle verdier. Lineær, forholdsmessig og den såkalte hybrid-modellen fra Oslo kommune med «knekk-punkt», har fått enda en konkurrent: Den hittil ukjente «Mø-metoden».
Men størst av alt er forutberegneligheten
Det finnes egentlig en jungel av formler som kan gi deg akkurat det resultatet du ønsker deg. Problemet er som regel forutberegneligheten. For at en konkurranse skal være forutberegnelig, bør du helst si på forhånd hvilke formler du vil bruke til å gi poeng.
Mø-metoden er lite forutberegnelig – med mindre du har forklart den på forhånd, selvsagt.
Men skjønnsmessig er den ikke. Så gjenstår jo spørsmålet om KOFA faktisk hadde rett, og tallet sju som score på 950.000 ikke ble satt på grunn av en formel, men rett og slett fordi det «føltes riktig». Det er ihvertfall slik KOFA konkluderer: «Innklagede har dermed brutt regelverket ved at poenggivningen på pris ikke var forutberegnelig og etterprøvbar, men fremstår vilkårlig«, sier de.
Men var ikke dette litt gøy uansett da? Hvem kommer til å bruke «Mø-metoden» til å beregne pris i sin neste anskaffelse? Har du oppgitt ku-formelen på forhånd, så vil den jo både være forutberegnelig og etterprøvbar.
Den som anskaffer får se.



